TQC+ Python 第2版|第一章「基本認識」詳解答案
BY PJ.
-2025 年 6 月 23 日
(最後更新於: 2025 年 7 月 29 日)
本系列將以章節為單位,從第一章開始,逐步提供 TQC+ Python 程式語言 第2版 證照考試的重點習題與詳解,助你系統化地複習與練習。
TQC+ Python 證照
TQC+ Python 程式語言證照採「實作考題」的方式,測驗考生的基礎程式能力。
目前考試版本分為 Python3 與 Python 第2版:
- Python3:難度較低,適合初次考照者
- Python 第2版:題型更具深度,適合想進一步挑戰的同學
報名與更多資訊,請至官方網站:
TQC+ Python 報考連結
考試章節大綱
| ✅Python 第2版 考試章節 | Python3 考試章節 |
|---|---|
| 1. 基本認識 | 1. 基本程式設計 |
| 2. 選擇敘述與迴圈 | 2. 選擇敘述 |
| 3. 函式與陣列 | 3. 迴圈敘述 |
| 4. 字串與檔案處理 | 4. 進階控制流程 |
| 5. 綜合應用一 | 5. 函式 |
| 6. 綜合應用二 | 6. 串列的一維、二維與多維運用 |
| 7. 綜合應用三 | 7. 數組、集合與詞典 |
| — | 8. 字串處理 |
| — | 9. 檔案與異常處理 |
提醒:
1. 購買參考書前,務必對照目錄,確認章節與官方考綱一致。
2. 考試除習題外,也會考綜合範例
習題 1:華氏攝氏溫度轉換
-
題目描述
請撰寫一程式,讓使用者輸入華氏溫度(degrees Fahrenheit),然後輸出其對應的攝氏溫度(degrees Celsius),輸出值請四捨五入至小數點後第二位。 -
輸入輸出
(a) 輸入說明:一個數值
(b) 輸出說明:轉換後的攝氏溫度(四捨五入至小數點後第二位) -
範例
提示:攝氏溫度 = (華氏溫度 − 32) × 5/9
參考解法
Fdegree = eval(input("請輸入華氏溫度:"))
Cdegree = ( Fdegree - 32 ) * 5 / 9
print(f"轉換後的攝氏溫度:{Cdegree:.2f}")
習題 2:計算 BMI
- 題目描述
請撰寫一程式,讓使用者輸入身高(cm)與體重(kg),然後輸出其對應的 BMI 值(四捨五入至小數點後第二位)。 -
輸入輸出
(a) 輸入說明:兩個數值
(b) 輸出說明:BMI 值(四捨五入至小數點後第二位) -
範例
提示:BMI = 體重(kg) / 身高²(m)
參考解法
hw = input("請輸入身高(cm)、體重(kg),輸入值以逗點隔開:")
h,w = hw.split(",")
weight = eval(w)
height = (eval(h) / 100)
BMI = weight / height ** 2
print(f"BMI = {BMI:.2f}")
習題 3:歐德斯猜想
- 題目描述
請撰寫一程式,讓使用者輸入一個大於 1 的整數n,以及三個正整數x, y, z,並驗證其是否滿足「歐德斯猜想」,亦即是否滿足下列式子:
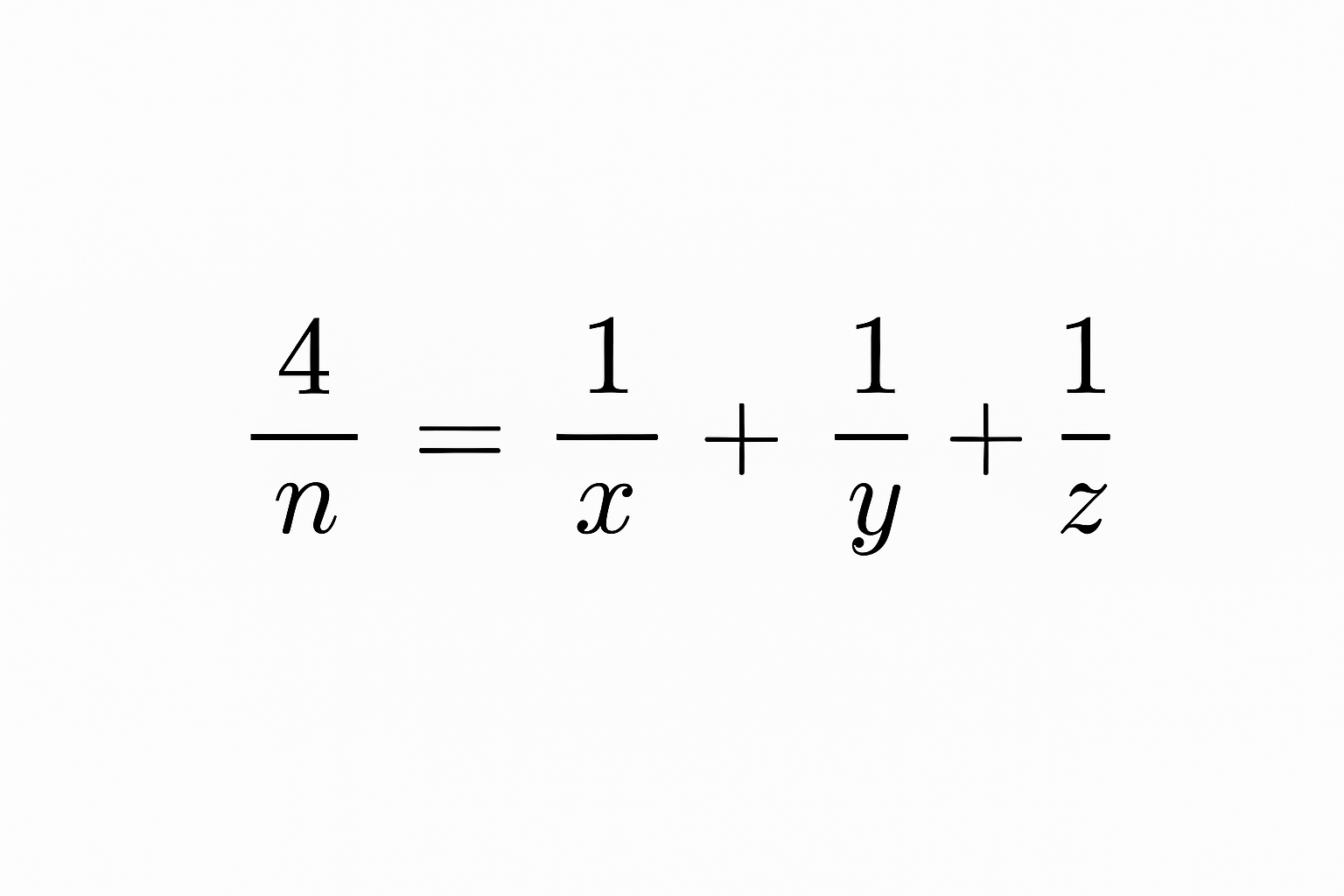
-
輸入輸出
(a) 輸入說明:一個大於 1 的整數 n,以及三個正整數 x, y, z
(b) 輸出說明:滿足「歐德斯猜想」則輸出 True,否則輸出 False -
範例
參考解法
n = eval(input("請輸入一個大於1的整數:"))
x, y, z = input("請輸入三個正整數,以逗點隔開:").split(",")
l = 4 / n
r = 1 / int(x) + 1 / int(y) + 1 / int(z)
print(l == r)
習題 4:計算導數值
- 題目描述
請撰寫一程式,讓使用者輸入一個數 a,並給定一個函數 f(x) 如下,請計算 f(x) 在 x = a 的導數值(derivative)。
.png)
注意:請利用導數的極限定義來計算,勿直接將導數寫在程式碼裡。
-
輸入輸出
(a) 輸入說明:一個數值 a
(b) 輸出說明:函數 f(x) 在 x = a 的導數值 -
範例
- 提示
若函數 f(x) 於 x = a 有定義,且以下極限存在,則 f(x) 在 x = a 的導數值為:
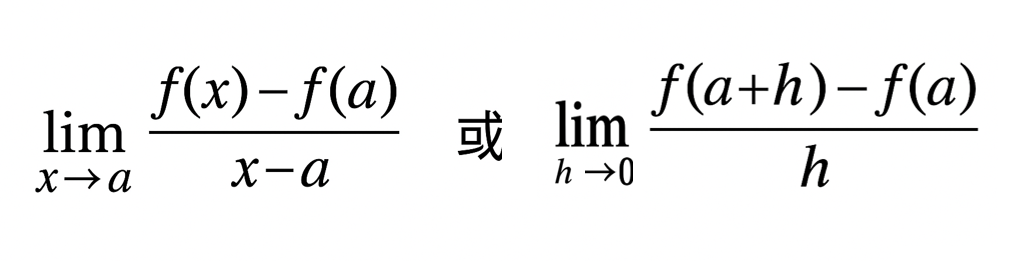
參考解法
def f_func(x):
fx = 3 * x ** 4 - 7 * x ** 2 + 5
return fx
def derivative(a,h=1e-8):
y = ( f_func(a+h) - f_func(a) ) / h # 根據極限定義 lim_{h→0} (f(a+h)-f(a))/h
return y
a = float(input("請輸入數值:"))
ans = derivative(a)
print("導數值 = ", ans)

